Con el fin de contribuir en aportes que hagan frente al COVID-19, un equipo de profesionales e investigadores pertenecientes a distintas facultades e institutos de la UNCUYO y del CONICET avanza en el desarrollo de estrategias para evitar el colapso del sistema de salud local. Lo hacen a través un modelo matemático que busca estimar la evolución de la pandemia en Mendoza teniendo como variables la cantidad de casos iniciales, la disponibilidad de camas y respiradores de las diferentes zonas de la provincia y la intercomunicación entre ellas.
Liderado por Cristian Sánchez y Luis Mayorga, el grupo de científicos trabaja de manera interdisciplinaria, ya que está integrado por químicos, médicos, biólogos, licenciados en sistemas, farmacéuticos y bioquímicos. Son miembros de la Facultad de Ciencias Exactas y Naturales de la Universidad y de los siguientes Institutos: Interdisciplinario de Ciencias Básicas (ICB-CONICET, UNCuyo); de Histología y Embriología de Mendoza (IHEM-CONICET, UNCuyo), de Medicina y Biología Experimental de Cuyo (IMBECU-CONICET, UNCuyo) y de Química Biológica de la Facultad de Ciencias Exactas y Naturales de Buenos Aires (IQUIBICEN, CONICET).
Reformulaciones y aportes
Según explicaron los profesionales a cargo, al inicio de la investigación consideraron la importancia de incluir a los pacientes asintomáticos o con síntomas muy leves en el modelo que adoptaron. La inquietud les surgió al comparar la tasa de mortalidad de Argentina ~3% con la tasa de mortalidad de países como Islandia ~0,3%, en donde se realizan tests diagnósticos a personas con y sin síntomas. “Indudablemente, la pluralidad de los infectados no cumple con los criterios clínicos que utiliza hoy Argentina para testear. De estos cálculos surgió que la gran mayoría (~90%) de los infectados en Argentina no se diagnostican por ser asintomáticos o tener síntomas muy leves. A pesar de que se considera que estos individuos tienen un número de reproducción o R0 (cuántas personas pueden ser infectadas por un portador) y un tiempo de contagiosidad de la mitad de los sintomáticos, y que son el motor de progresión de la pandemia porque no se detectan ni aíslan”, detallan.
A pesar de que en un principio se habían propuesto simular estrategias de supresión, detectaron como mejor escenario posible que estas supresiones se activen según la ocupación de camas de terapia intensiva (UTI) y combinarlo con la detección y aislamiento de individuos asintomáticos. Esto, afirman, reduciría notablemente el número efectivo de reproducción, la carga sanitaria y la mortalidad general.
“En el supuesto ideal de que la mitad de los asintomáticos o pacientes muy leves pudieran detectarse y aislarse, no habría necesidad de cuarentena en Mendoza y el sistema de salud no colapsaría. La detección y el aislamiento de todas las personas infectadas, sin dejar de lado al grupo asintomático, es la clave para superar esta pandemia”, advierten.
Con respecto a las medidas preventivas, expresan: “en general, como esperábamos, en las simulaciones que llevamos a cabo las estrategias fueron notablemente más efectivas cuando las medidas de mitigación, como higiene, distanciamiento social y prohibición de aglomerados no se relajaron entre las acciones supresoras, la cuarentena general”.
Sobre el modelo aplicado
El modelo matemático funciona introduciendo parámetros precisos de la enfermedad. Por ejemplo, el periodo de incubación, la infectividad del virus o el tiempo que demora en recuperarse un paciente. Estos datos son obtenidos de la experiencia de países que ya han atravesado la pandemia. También se considera la proporción esperada de casos asintomáticos, sintomáticos leves y severos.
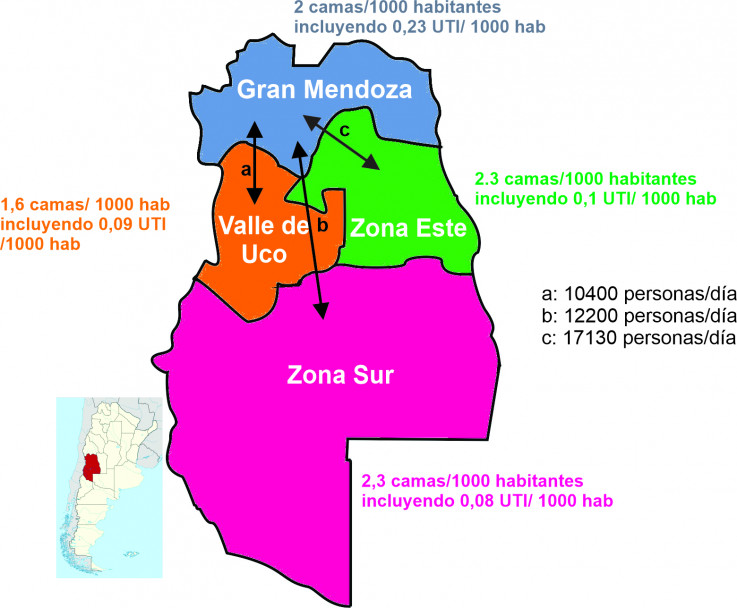
En cuanto a diferencias técnicas con otros modelos, explican: “elaboramos un modelo de tipo SEIR (Susceptibles-> Expuestos-> Infectados-> Recuperados) en donde los sintomáticos y asintomáticos se mueven en compartimentos diferentes. Introdujimos parámetros de carga sanitaria que permiten inferir posibles estrategias de contención y supresión. El modelo se amplió para describir también diferentes áreas interconectadas (Gran Mendoza, Valle de Uco, zona Sur y zona Este), dando la posibilidad de activar medidas regionalizadas. Se ajustó especialmente a los parámetros de Mendoza, pero es adaptable a cualquier lugar del mundo”.
Debido al dinamismo y a la actualización constante de los datos sobre esta enfermedad, los científicos continúan perfeccionando los parámetros del modelo matemático para proporcionar escenarios hipotéticos aún más precisos de cómo podría ser el futuro de la pandemia en Mendoza. Los resultados y herramientas obtenidos hasta ahora se encuentran disponibles en: https://www.medrxiv.org/content/10.1101/2020.04.23.20077255v1.article-info
Nuevos aportes a la detección de casos
En línea con esta investigación de la UNCUYO, otro grupo de científicos liderados por María Roqué (IHEM y FCEN) se encuentra diseñando una modalidad de testeo de muestras agrupadas en “pooles”. Esto se basa en la mezcla de muestras para realizar una única detección (por RT-PCR). Si esta es negativa se consideran todas negativas, y si la mezcla resulta positiva, se desglosa en partes para detectar al o los individuos infectados.
El aporte, que hoy está en la instancia de puesta a punto de la técnica, contribuiría a disminuir la cantidad de insumos y ensayos requeridos en el orden de 30 a 100 veces. Este método podría servir para monitorear la presencia de asintomáticos en la población sin implicar un costo excesivo y que fue muy efectivo en Israel.